-
\( f(x) = e^x \) の 導関数を求めよ
-
導関数の定義
\begin{align}f'(x) = \lim_{h \rightarrow 0} \frac{f( x+{h } ) - f(x)}{h }\end{align}
いま、関数が
\begin{align} f(x) = e^x
\end{align}
で、$x$ を「記入欄」だと思えば
\begin{align} f( ) = e^{( )}
\end{align}
なので、( )に$x+h$を代入すれば
\begin{align} f( x+h ) = e^{x+h}
\end{align}
これらを導関数の式に代入すれば
\begin{align}f'(x)
&=& \lim_{h \rightarrow 0} \frac{f( x+{h } ) - f(x)}{h }\\
\\
&=& \lim_{h \rightarrow 0} \frac{ \quad \quad e^{x+h} - e^x \quad }{h }
\end{align}
指数関数の法則より$ e^{x+h} = e^x\cdot e^h$なので
\begin{align}f'(x)
&=& \lim_{h \rightarrow 0} \frac{ \quad \quad e^x\cdot e^h - e^x \quad }{h }
\end{align}
分子の後半の $e^x$ を $e^x \cdot 1 $ と考えて
\begin{align}f'(x)
&=& \lim_{h \rightarrow 0} \frac{ \quad \quad e^x\cdot e^h - e^x \cdot 1 \quad }{h }
\end{align}
分子には全部に$e^x$がかかっているので、これを外に出すように因数分解
\begin{align}f'(x)
&=& \lim_{h \rightarrow 0} \frac{ \quad e^x ( e^h - 1 )\quad }{h }
\end{align}
$e^x$ は $h$ とは直接関係ないので、 $\lim$ の外に出してもかまわない
\begin{align}f'(x)
&=& e^x \lim_{h \rightarrow 0} \frac{ \quad ( e^h - 1 )\quad }{h }
\end{align}
| |
-
ここで、 $e$ の定義より
\begin{align}
\lim_{h \rightarrow 0} \frac{ \quad \quad e^h - 1 \quad }{h } \equiv 1
\end{align}
| |
-
なので
\begin{align}f'(x)
&=& e^x \cdot 1 \\
&=& e^x \quad
\end{align}
以上まとめると、
\( f(x) = e^x \) の 導関数 \( f'(x) = e^x \)
つまり $(e^x)' = e^x$ 微分しても同じ
そりゃそうだよね!そうなるように、 $e$ を決めたのでした。
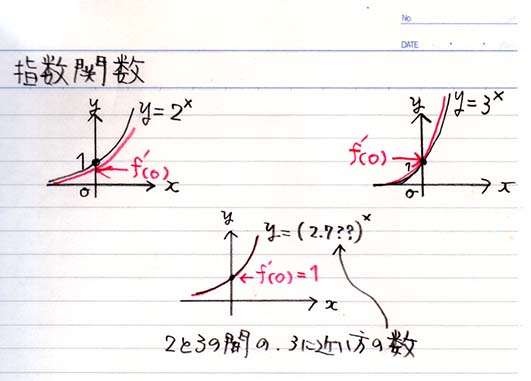
ではやりかたがわかったところで
-
\( f(x) = e^{3x} \) の 導関数を求めよ
-
できたら次のページ
|
