-
そして思うわけです。
\(f(x) = 2^x\) は増加率が下、
\(f(x) = 3^x\) は増加率がちょっと上なら
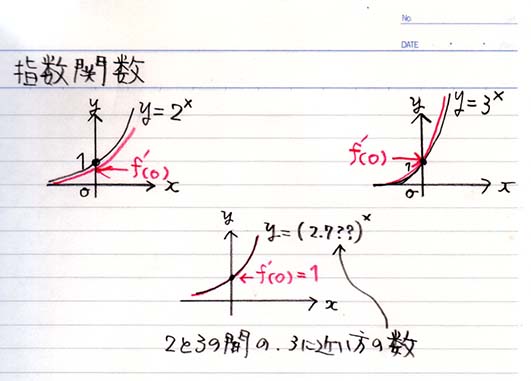
2と3の間のどこか
\( 2.5^x\) とか
\( 2.6^x\) とか
\( 2.7^x\) とか で、
元のグラフと増加率とぴったり重なるとこがあるのでは?
( \(3^x\) のほうが黒線と赤線が近かったので、たぶん3に近いほう)
そしてそこでは、
$x=0$における微分係数 \(f'(0)\) がちょうど1なのでは!?
この状況も、ノートにイラストっぽく描いてください。
「2と3の間で3に近いほうの数で黒線と赤線が重なるやつ」では今後大変なので、
円周率に$\pi$と名前を付けたように、これにも名前を付けたいです。
-
自然対数の底 e
-
この「2と3の間で3に近いほうの数」のことを $e$ と書き、
「ネピア(Napier)数」とか「自然対数の底(てい)」と呼びます。
定義は
\( f(x) = e^x\) のとき
\( f'(0) = 1\)
となる数が $e$ です。
$e$ の値は2.71くらいです(教科書p28)。
-
指数関数
-
そしてこの
\( f(x) = e^x\) を指数関数 (exponential function) と呼びます。
大人は \( f(x) = exp(x)\) と書くこともあります。同じ意味です。
理工系に限らずどんな分野でも重要な関数です。
情報通信工学科の皆さんは、この指数関数を使いまくって勉強していきます。
-
x=0 における微分係数が1
-
$x=0$ における微分係数は
-
\begin{align}f'(0) = \lim_{\Delta x\rightarrow 0} \frac{f( 0+{\Delta x} ) - f(0)}{\Delta x}\end{align}
でした。\(\Delta x\) かくのがめんどくさいので $h$ を使って書くと
-
\begin{align}f'(0) = \lim_{h \rightarrow 0} \frac{f( 0+{h } ) - f(0)}{h }\end{align}
でもいいです。どっちでも同じです。
いま、関数が
\begin{align} f(x) = e^x
\end{align}
で、$x$ を「記入欄」だと思えば
\begin{align} f( ) = e^{( )}
\end{align}
なので、( )に0を代入すれば
\begin{align} f( 0 ) = e^0 = 1
\end{align}
( )に$h+0$を代入すれば
\begin{align} f( 0+h ) = e^{0+h} = e^h
\end{align}
ですよね。
これらを$x=0$ における微分係数の式に代入すれば
\begin{align}f'(0)
&=& \lim_{h \rightarrow 0} \frac{f( 0+{h } ) - f(0)}{h }\\
\\
&=& \lim_{h \rightarrow 0} \frac{ \quad \quad e^h - 1 \quad }{h }
\end{align}
になりますね。これが「1になる」というのが、 $e$ の定義です。なので
\begin{align}
\lim_{h \rightarrow 0} \frac{ \quad \quad e^h - 1 \quad }{h } \equiv 1
\end{align}
と書けます。(教科書p54)
「=」でなく3本線の「$\equiv$」をかいたのは、
「計算したら1になった」ではなくて
「これが1になるように定義した」ということを表しています。
(「=」を使って書いても間違いではないので安心してください)
この式を、いろいろな式の導出に使っていきます。
できたら次のページ
|
