-
\(
f(x) = 3^x\) のグラフ(黒線)と増加率 \( \frac{\Delta y}{\Delta x}\) のグラフ(赤線)
-
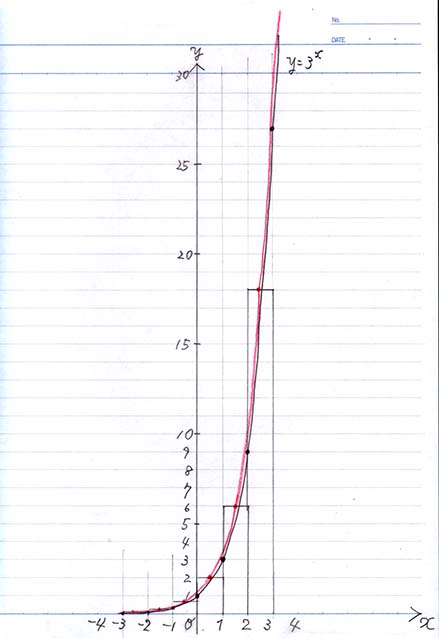
赤線が増加率です。ほんのわずかに、
元のグラフより上でした!
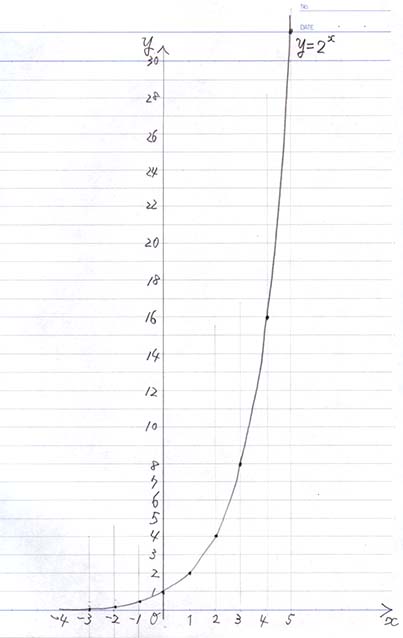
では同じことを、今度は \( 2^x\) でやってみましょう。
-
\(f(x) = 2^x\) のグラフと増加率 \( \frac{\Delta y}{\Delta x}\) のグラフ
-
今度はもう最初から重ねて棒グラフ書いていいです。
例:
$x=0$ から $x = 1$ までの区間では
$y=1$ から $y=2$までなので
\(\Delta y = 2-1 = 1\)
$x=-1$ から $x = 0$ までの区間では
$y=2^{-1}$ から $y=1$までなので
\(\Delta y = 1-\frac{1}{2} = \frac{1}{2}\)
$x=-2$ から $x = -1$ までの区間では
$y=2^{-2}$ から $y=2^{-1}$までなので
\(\Delta y = \frac{1}{2}- \frac{1}{4} = \frac{1}{4}\)
:
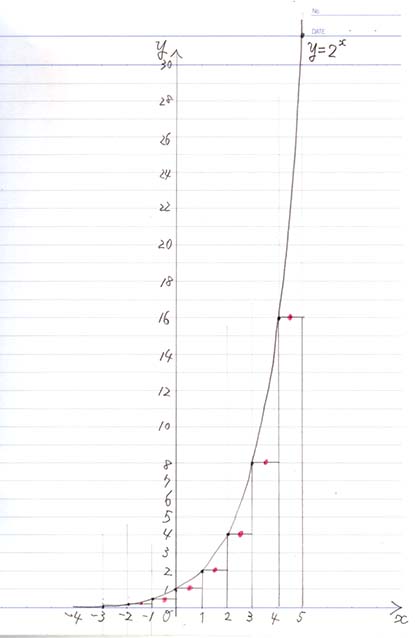
かいたら
棒グラフの横線の真ん中を赤線で丁寧につないでください。
赤線と黒線は重なる?
できたら次のページ
|


