-
\(f(x) = 2^x\) のグラフ(黒線)と増加率 \( \frac{\Delta y}{\Delta x}\) のグラフ(赤線)
-
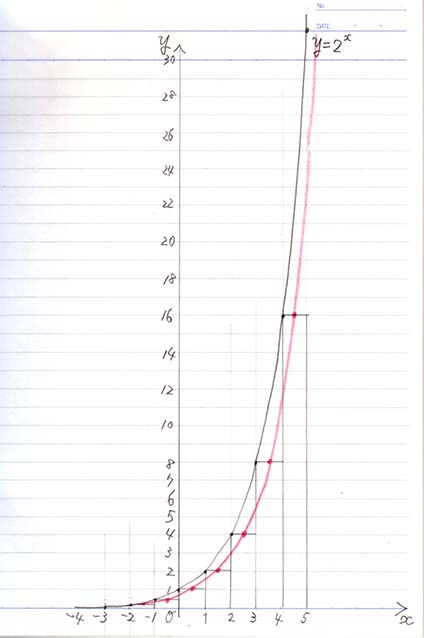
赤線が増加率です。 元のグラフより わりと下でした!
\(f(x) = 2^x\) と \(f(x) = 3^x\) 比べてみましょう
\(f(x) = 2^x\) は増加率が下、 \(f(x) = 3^x\) は増加率がちょっと上

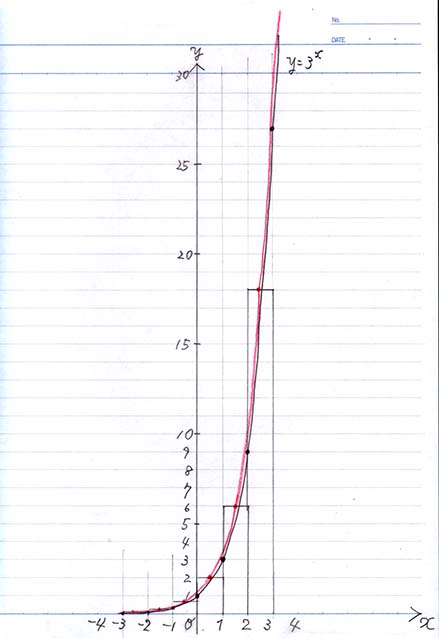
増加率をくわしくしたものが微分係数なので、
たとえば$x=0$のところをみれば
\(f(x) = 2^x\) の$x=0$における微分係数 \(f'(0)\) は $f(0)=2^0$ より下
\(f(x) = 3^x\) の$x=0$における微分係数 \(f'(0)\) は $f(0)=3^0$ より下
この状況を、ノートの新しいページに、
イラストっぽく描いてください。
左に \(f(x) = 2^x\) 、真ん中を空けて、右に \(f(x) = 3^x\)
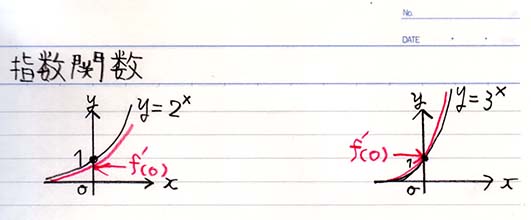
\( 2^x\) は 赤線が下、 \(f'(0)\) が1未満 \( 3^x\) は 赤線が上、 \(f'(0)\) が1以上
できたら次のページ