| ラプラス変換 |
| 回路の説明に戻る
例題(LC回路) 抵抗なし |
インダクタンスLのコイル、電気容量Cのコンデンサ を電源に直列につないだときの
インパルス応答を求めよ
|
これは飛ばして 次の問題へ進む |
|
電気用図記号 変わります |
|
|
||
|
|
|
微分法則 ( y’ )
= ( y’ )
= - y(0) + s  ( y ) ( y )
|
|
|
|
微分法則 ( y’ )
= ( y’ )
= - y(0) + s  ( y ) ( y ) |
|
|
|
( Ls + 1/Cs )は 「特性関数」 または 「インピーダンス」 |
|
|
|
単位インパルス 単位関数 インパルス応答 単位応答 |
|
|
|
左の式は  ( i )
= ( Ls + 1/Cs )-1 ( i )
= ( Ls + 1/Cs )-1ともかけるね。 この( Ls + 1/Cs )-1を 「伝達関数」と いいます 今、 i は インパルス応答だから  ( インパルス応答 )= ( インパルス応答 )= ( 伝達関数 ) |
|
検算しましょう |
出来た答えを微分して元の方程式に代入し、成り立つかどうか確かめよう。
i(t) = (1/L)・cos(ωt) ただし ω = √(1/LC) だから i'(t) = - (ω/L)・sin(ωt) = -1/L√(LC)・sin(ωt) q(t) = ∫i(t)dt = 1/(Lω)・sin(ωt) = √(C/L)・sin(ωt) (積分定数は0にしました) 元の方程式 L di(t)/dt + q(t)/C に代入すると = 0 これは t>0 での E(t)= δ(t)と同じなのでOK 初期条件も代入してみよう。 q(0) = 0 これはOK。だけど i(0) = (1/L)・cos(0) = 1/L 合いませんよ!? 実は、 インパルス応答のときは t=0 を代入して成り立たないこともあります。 インパルス応答というのは、 t=0 の瞬間を表現するにはちと無理があるのです。 | |
|
解を味わう |
今回得られた解はすごい! どこがすごいって、電源に波なんか入れてないのに、 こういう電圧(一瞬だけONであとOFF)に対し E  t ti(t)= (1/L)・cos(ωt)っていう、 振動する電流が流れるんですよ! i(t) 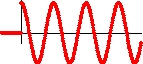 t tすごくないですか!? 電源が振動してたわけじゃなく、 この回路は、この回路の個性として、 この周波数で振動したいんですよ! 電圧ONになったのは一瞬だけで、あとずっと電圧ゼロなのに、 電流はずーっとなくならないで続いてるし! さらに、この波の角周波数ω = √(1/LC)なので、 LとCを調整すれば、好きな周波数の波にできるんですよ! |
小学生的に考えると、 こういう電圧なら E  t tこういう電流って思ったりしません? i  t tそれとも、小学生だったら 「コンデンサのとこで電線が切れてるから電流流れない」かな? |
|
|
次の問題へ進む
「初心者用ラプラス変換解説」最初のページへ戻る |
回路の問題一覧 合成法則  (f) (f) (g) へ進む (g) へ進む |
 の両端の電圧
L di(t)/dt,
コンデンサ
の両端の電圧
L di(t)/dt,
コンデンサ  の両端の電圧
q(t)/C,
合計が 電源の起電力E(t)と等しくなるので、
の両端の電圧
q(t)/C,
合計が 電源の起電力E(t)と等しくなるので、