- 合成関数の微分$\displaystyle y'={ dy \over du} { du\over dx}$ の導出やりなおし(教科書p44)
前のページで \begin{align} y = \sin( x^3 +x^2 +1) \end{align} という、1本の複雑な式を、 \begin{array}{ll} u &= x^3 +x^2 +1 \\ y &= \sin{( u )} \end{array} という、2本の簡単な式に書き換えましたよね。
同じように \begin{align} y = g( f(x) ) \end{align} という、1本の複雑な式(合成関数)を、$u$ を仲介にして \begin{array}{ll} u &= f(x) \qquad (x が決まれば u がわかる) \\ y &= g( u ) \qquad (u が決まれば y がわかる) \end{array} とかいて、2本の簡単な式にばらします。
この $g( u ) $ を $u$ で微分すると \begin{align} {dg \over du } = \lim_{ \Delta u \rightarrow 0}{g(u +\Delta u) -g(u) \over \Delta u } \end{align} と書けます。
この式が $\displaystyle {dg \over du } $ になるのは $\displaystyle \lim_{ \Delta u \rightarrow 0}$ があるからで、
もしこれがなかったならば、
$\displaystyle {g(u +\Delta u) -g(u) \over \Delta u } $ の値は $\displaystyle {dg \over du } $ の値からは ズレているはずです。
$\displaystyle \lim_{ \Delta u \rightarrow 0}$ なしで書いてみると \begin{align} {g(u +\Delta u) -g(u) \over \Delta u } = {dg \over du } + ズレ \end{align}
$ \Delta u \rightarrow 0 $ のとき ズレは 0 になるはず。
ということはズレの値は $ \Delta u$ によって変わるので、
オーという名前の $ \Delta u$ の関数として $O(\Delta u)$ と書くことにします。
\begin{align} {g(u +\Delta u) -g(u) \over \Delta u } = {dg \over du } + ズレO(\Delta u) \end{align} ただし $ \Delta u \rightarrow 0 $ のときズレ$O(\Delta u)\rightarrow 0 $
この式の両辺に$ \Delta u$ を掛けると \begin{align} g(u +\Delta u) -g(u) = \left( {dg \over du } + ズレO(\Delta u) \right) \Delta u \end{align} と書くことができます。
この状態で、 \begin{array}{ll} u &= f(x) \\ y &= g( u ) \end{array} の $y$ の微分を考えます。 \begin{align} {dy \over dx } = \lim_{ \Delta x \rightarrow 0}{g(u+ \Delta u) - g(u) \over \Delta x } \end{align} この式の分子に、さっき上で求めた式を代入 \begin{align} {dy \over dx } &= \lim_{ \Delta x \rightarrow 0}{ \left( {dg \over du } + ズレO(\Delta u) \right) \Delta u \over \Delta x } \\ \\ &= \lim_{ \Delta x \rightarrow 0} \left( {dg \over du } + ズレO(\Delta u) \right) {\Delta u \over \Delta x } \end{align} $ \Delta x \rightarrow 0 $ のときは $ \Delta u \rightarrow 0 $ なので $O(\Delta u)\rightarrow 0 $
また ${\Delta u \over \Delta x } \rightarrow { du \over dx}$ なので \begin{align} {dy \over dx } = {dg \over du } { du \over dx} \end{align} $y = g(u) $ なので \begin{align} {dy \over dx } = {dy \over du } { du \over dx} \end{align} と導出できました。(教科書p.45)
回りくどい感じがしますが、 $\Delta u $ が分母に出てこないので
破綻は回避できます。
教科書p.44 の枠の中の右側にこの式があるので、
右辺の2か所の$du$ に色を付けてください。
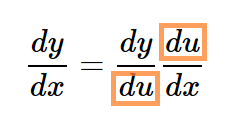
この式を見ると、$x$ から直接 $y$ に行かないで、
$u$ に間を取り持ってもらって、
$x$ から $u$, $u$ から $y$ に行っている事が分かります。
問題に進む