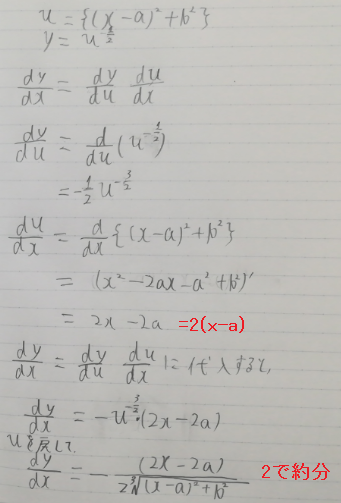- 課題その2:ここが1文字だったらと思うところを$u$と置いて合成関数の微分
-
(1)-(4)教科書 p.46、(5)-(6) p.49
で答え合わせ
-
注:
教科書では、ページ数節約のため途中を省略して書いてありますが、
皆さんは途中を省略しないで丁寧に書いてください。
必ず
$\displaystyle
{dy \over dx } = {dy \over du } { du \over dx}
$のように書いてください。
$y'=y'u'$ と書くと誤りです。最初の $'$ と次の $'$ の違いが判りません。
-
(7) $y = \tan( x^2 + 1 )$
-
完璧

-
(8)
$\displaystyle y = {1 \over \sqrt{(x-a)^2 + b^2 }} \qquad$ ただし $ a, b $ は定数
-
惜しい

なお 2行め「u= と置くと」の式と「y= 」の式は改行して
それぞれ1行使ってください
惜しい
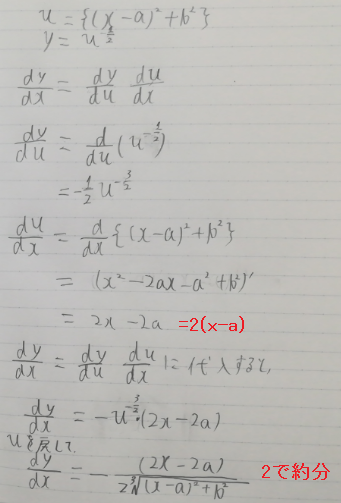
2で約分してたら完璧
良くある間違い

最後の行、展開して足し算になってしまったところに( )がないので
足し算より掛け算優先のため、間違いとなっています。
展開しないほうが短いし見やすいし見通しが良いのに、
どうして展開するのでしょう?
よくある作戦ミス

ルートがついたまま u と置いてしまうと、
u の微分が楽になりません。
せっかくなら、ルートの中身だけを u
と置くほうが楽ですね。
じぶんの答案を見比べて、間違っている所は赤ペンで修正、
一人で解けるようになるまでやり直してください。
もくじ
|