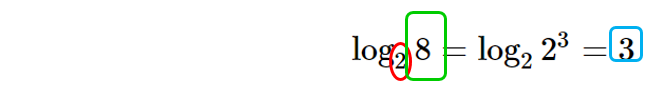-
\begin{align}
&2^{\, 5} &=& \quad 32\\
&2^{\, 4} &=& \quad 16 \\
&2^{\, 3} &=& \quad 8\\
&2^{\, 2} &=& \quad 4\\
&2^{\, 1} &=& \quad 2\\
&2^{\, 0} &=& \quad 1\\
&2^{-1} &=& \quad {1 \over 2}\\
&2^{-2} &=& \quad {1 \over 4}\\
&2^{-3} &=& \quad {1 \over 8}\\
\end{align}
簡単だよね
ただこの問題のように
\begin{align}
&2^{\,(\qquad )} &=& \quad 32\\
\end{align}
2を何乗したら32 になりますか?って聞きたいときに、
いちいち空欄を作って記入してもらうのでは大変ですよね。
今までは
\begin{align}
2^{\, x} &=& \quad y \\
\end{align}
$x$ を入れて $y$ を求めてたんですが、逆に
$y$ から $x$ を求めたいとき、なんか書き方ないでしょうか。
そういう目的のために開発されたのが $\log$ (ログ、日本語でいうと対数)です。
- 対数($\log$)(教科書p.29)
-
\begin{align}
2^{\, x} &=& y \qquad 書き直すと \quad
\log _2{y } = x
\end{align}
意味は、$y$ は 2 の何乗ですか? (答え: $x$ 乗です。) ってこと
2 をベースに考え、肩の上の数 $x$ を求める関数です。
例です。
\begin{align}
\log _5{25 } =
\end{align}
25 は 5 の何乗ですか?ってこと。もちろん2乗だよね
\begin{align}
\log _5{25 } =
\log _5{5^2 } = 2
\end{align}
肩の上を答えればよいのです。
ここで、「 の何乗」のベースになっている
2 とか
5 とかのことを
ベース(base)といいます。そのまんまですね。
日本語だと「底(てい)」といいます。ベース、一番下だから「底」?
そして、
y とか
25 とかのことを「真数」といいます。
「2の何乗」とか
「5の何乗」とかなので、
プラスの数を何回かえてもプラスだから、真数はプラスの数です。
-
ノートに書くときは
-
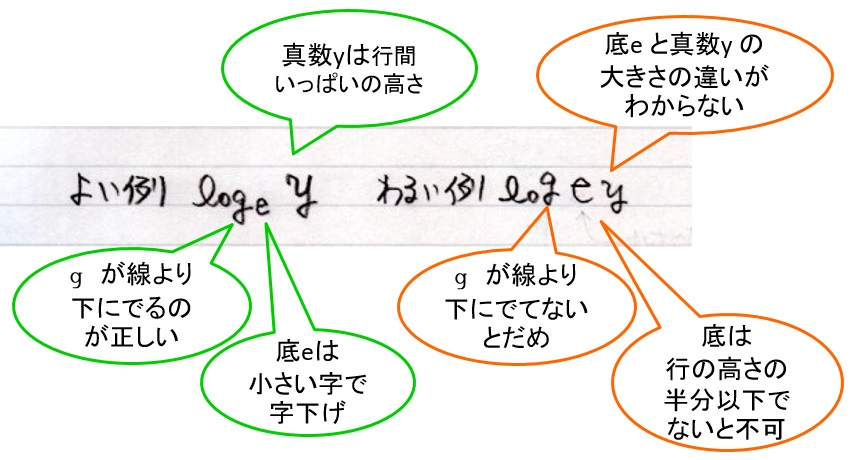
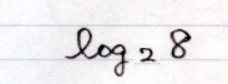 のようにかいてください。 のようにかいてください。
$\ell$は行の高さいっぱい、o は行の高さの半分、
gの玉はoと同じ大きさで、足が罫線より下に出るように書く。
「底 2」は $\log$ よりも小さい字で、 $\log$ よりも少し下に書く。
その後ろの「真数 8」は $\log$ の $\ell$ と同じく行の高さいっぱいに書く。

- 練習
-
\begin{align}
\log _2{8 } =
\end{align}
8 は 2の何乗ですかってこと。
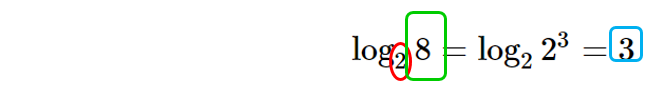
肩の上を答えればよいのです。
\begin{align}
\log _2{32 } =
\end{align}
\begin{align}
\log _3{27 } =
\end{align}
\begin{align}
\log _{10}{100 } =
\end{align}
\begin{align}
\log _3{({1\over 3}) } =
\log _3{(3^{-1} ) } =
\end{align}
\begin{align}
\log _{10}{0.1 } =
\log _{10}{({1\over 10 })} =
\end{align}
かいたら答え合わせ
|
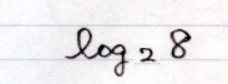 のようにかいてください。
のようにかいてください。