-
$\log$の出てこない形に直しなさい
\begin{align}
\log _e{y } = -x^2
\end{align}
底が $e$、 肩の上が$-x^2 $ なので
\begin{align}
y=e^{-x^2 }
\end{align}
かんたんでした。ここで、
- 教科書p.34をみてください。
底にもいろいろありますが、いちばんよく使うのは 10 と $e$ です。
10はなんとなくわかりますよね。
\begin{align}
\log _{10}{y } = x \qquad 直すと \qquad y= 10^x
\end{align}
何桁あるか調べる時に必要ですね。
5000円だと思ったら 50000円だった、とか
0が1個多いか少ないかでだいぶ違いますもんね。
理工系に限らず一般の人(common people) も使う対数なので
これを「常用対数(common logarithm)」と呼び、
lc y とも書きます。でも使ってるのをあまり見たことないです。ふつうは
$
\displaystyle
\log _{10}{y }
$
でいいです。
- 自然対数
底が $e$ の対数
\begin{align}
\log _{e}{y } = x \qquad 直すと \qquad y= e^x
\end{align}
は、理工系なら分野を問わずどこの学部学科でもとてもよく使います。
また、人口増加とか、感染の拡大とか、
自然の摂理に従って増加減少するときには必ず出てきます。
自然(natural)現象によく使うのでこれを自然対数(natural logarithm)といい、
ln y とも書きます。これはよく使います。
$\log _{e}{y } $ とかくには $e$ を小さい字の下付きにしないといけないので面倒ですが
ln y だけならメールででも送れます。
関数電卓にもあるよ。 ln が自然対数、log が常用対数
-


-
常用対数の log 押して 10 を入れると、$\log _{10}{10 } $なので1と出るはず。
自然対数の ln 押して 10 を入れると、$\log _{e}{10 } $なので2.302...となります。
また、 log 押して 1 でも、 ln 押して 1 でも、
$\log _{10}{1} = \log _{10}{10^0 }=0 $、
$\log _{e}{1} = \log _{e}{e^0 }=0 $ なので、どっちも0になりますね。
関数電卓は理工系学生の必需品です。実験や電気回路の試験で使います。
日頃はスマホの電卓でもよいですが、試験にはスマホ持ち込みできないので
使い慣れた関数電卓が必要になるでしょう。
- 再び 教科書p.34を見てください。
-
「$e$ を自然対数の底とも言う。」
の次の行に
「数学においては自然対数をよく使うので、その底 $e$ を省略して
\begin{align}
y= \log{x }
\end{align}
と書くことが多い。省略してあれば底は $e$ である。」
と書いてありますね。
ここでご注意です。よいこの皆さんは省略しないで底 $e$ を書いてください。
底 $e$ を省略するのは印刷屋さんの都合です。
皆さんが省略しても、何もいいことがありません。
例えば
\begin{align}
\log{e } =1
\end{align}
とあると、「どうして1なんですか」という質問が山ほど来ます。
\begin{align}
\log_e{e } =1
\end{align}
なら、当たり前じゃん?$e$ は $e$ の1乗ですもんね。
また、
\begin{align}
\log{y } =x \qquad を \qquad y= に直しなさい
\end{align}
と言われても「わかりません」「どうやるんですか」という質問が山ほど来ます。
\begin{align}
\log_e{y } =x \qquad を \qquad y= に直しなさい
\end{align}
なら簡単です。今後の専門科目では、こういう作業が多いのです。
わざわざわかりにくくしてまで、$e$ を省略するメリットがないです。
教科書で底が省略されているところには、自分で底 $e$ を記入してください。
例えばp.35 の総合演習1-1の1.の(9) に底がないですね。ここに
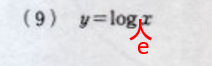 と底 $e$ を記入してください。 と底 $e$ を記入してください。
3.(2)も底がないですね。ここに
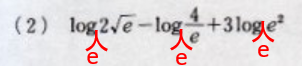 と底 $e$ を記入してください。 と底 $e$ を記入してください。
今後、底が省略されているところを見つけたら、全箇所、自分で底 $e$ を記入してください。
次へ
|


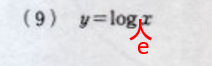 と底 $e$ を記入してください。
と底 $e$ を記入してください。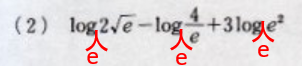 と底 $e$ を記入してください。
と底 $e$ を記入してください。